Skip to main content

Design Under Uncertainty

Over the past two decades, our lab has introduced methods for design under uncertainty to mitigate the effects of uncertainty, reduce the potential risks, and improve the product performance with low cost. In our research, two major sources of uncertainties in simulation-based design are considered: uncertainty due to natural or physical randomness, and uncertainty due to lack of knowledge or lack of simulation or experimental data. The associated research topics include uncertainty quantification, uncertainty propagation, uncertainty reduction, and decision-making under uncertainty. Example subjects of our widely cited works are metamodeling techniques for simulation-based design, optimal design of computer experiments, analytical statistical sensitivity analysis, robust design, reliability-based design, and sequential optimization & reliability analysis (SORA). Our most recent works cover resource allocation in variable-fidelity optimization, model calibration, validation and uncertainty quantification, and multidisciplinary optimization under uncertainty.

Representative Early Publications on Design under Uncertainty

Jump to

Metamodeling for Simulation-Based Design

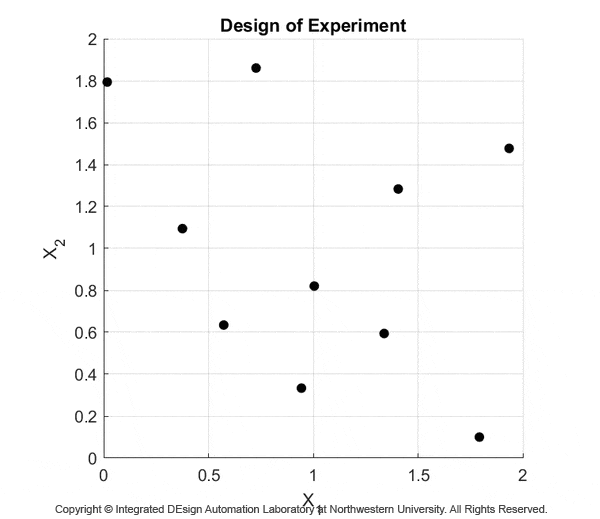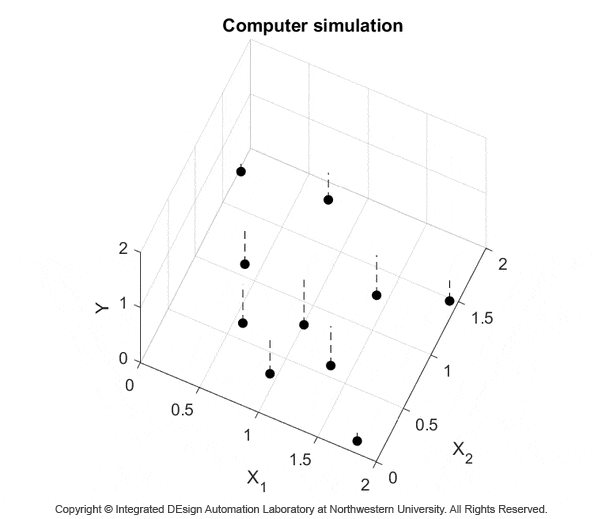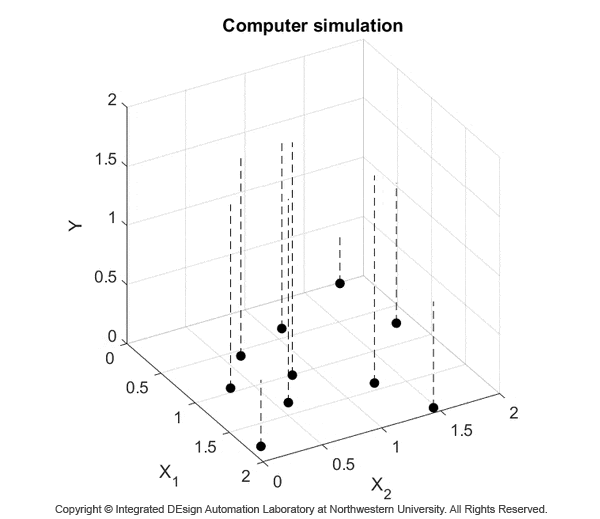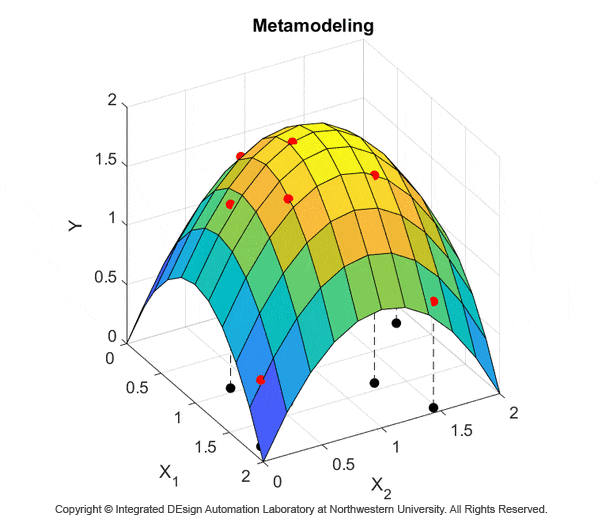Despite advances in computing power, the enormous computational cost of running physics-based simulations makes it impractical to rely exclusively on simulation for the purpose of engineering design. To alleviate the computational burden, our research in this area builds cheap-to-compute surrogate models (also called metamodels) to replace the original expensive models for simulation-based design. In our past research, comparative studies have been conducted to provide guidelines for choosing the most appropriate metamodeling technique based on multiple modeling criteria in both deterministic design and design under uncertainty. To improve the accuracy as well as the efficiency of using metamodeling techniques, adaptive objective-oriented sampling strategies have been developed for both global approximation of a design space and metamodeling for the purpose of design optimization. Analytical formulations have been derived for global sensitivity analysis and uncertainty propagation for a variety of metamodels. Our most recent developments include a Gaussian Process Modeling (GPM) technique for high-dimensional problems with highly nonlinear behavior, and flexible multi-model fusion methods capable of integrating heterogeneous information from variable-fidelity computational models and physical experiments. The benefits and potentials of our metamodeling techniques have been demonstrated through various design applications.

Representative papers

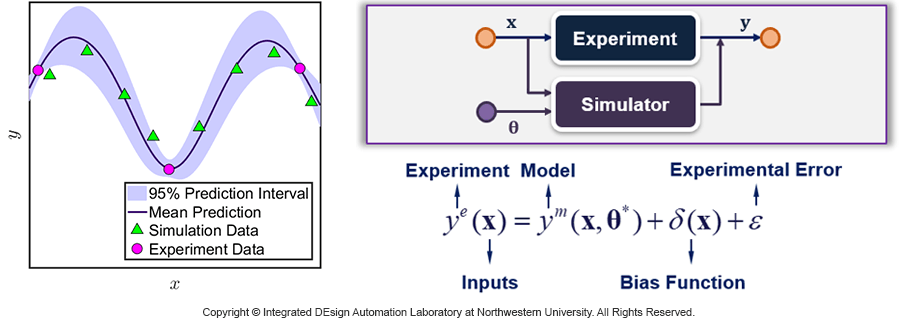
Model Validation and Uncertainty Quantification

Computational models play an increasingly important role in the analysis and design of modern engineering systems. All models need to be validated for their intended uses, given limited data/resources. In some cases, unknown model parameters need to be calibrated and model prediction uncertainty must be quantified. To this end, we have developed a model updating framework that combines both computer and physical experiments to improve the confidence of using predictive models in design, employing a Bayesian model calibration and uncertainty quantification approach. Further research topics include (1) validation metrics for given scenarios and intended uses, (2) design of physical experiments for cost reduction, and (3) improving the identifiability of model parameter uncertainty versus model discrepancy uncertainty. Our recent research works focus on developing methods for validating dynamic engineering models and validation/UQ of multiscale materials models.

Representative papers

Multidisciplinary Design Optimization (MDO) under Uncertainty

Modern engineering systems often contain multiple disciplines, the analyses of which are largely independent but coupled through linked and/or shared variables. All-in-one strategies for optimizing such systems are usually less efficient than distributed strategies, which decompose the all-in-one problem into discipline-wide sub-problems for discipline solvers to solve. To achieve the system design objectives most efficiently and effectively, we have developed

  1. multidisciplinary optimization architectures in both deterministic and probabilistic settings,
  2. uncertainty propagation and sensitivity analysis methods for multidisciplinary systems, and
  3. resource allocation strategies for uncertainty reduction in simulation-based multidisciplinary systems.

Representative papers

List of Publications

Copyright 2024 Integrated DEsign Automation Laboratory (IDEAL) at Northwestern University. All Rights Reserved.